

The Gauss-Jordan Elimination method is an algorithm to solve a linear system of equations. We can also use it to find the inverse of an invertible matrix. Let’s see the definition first:
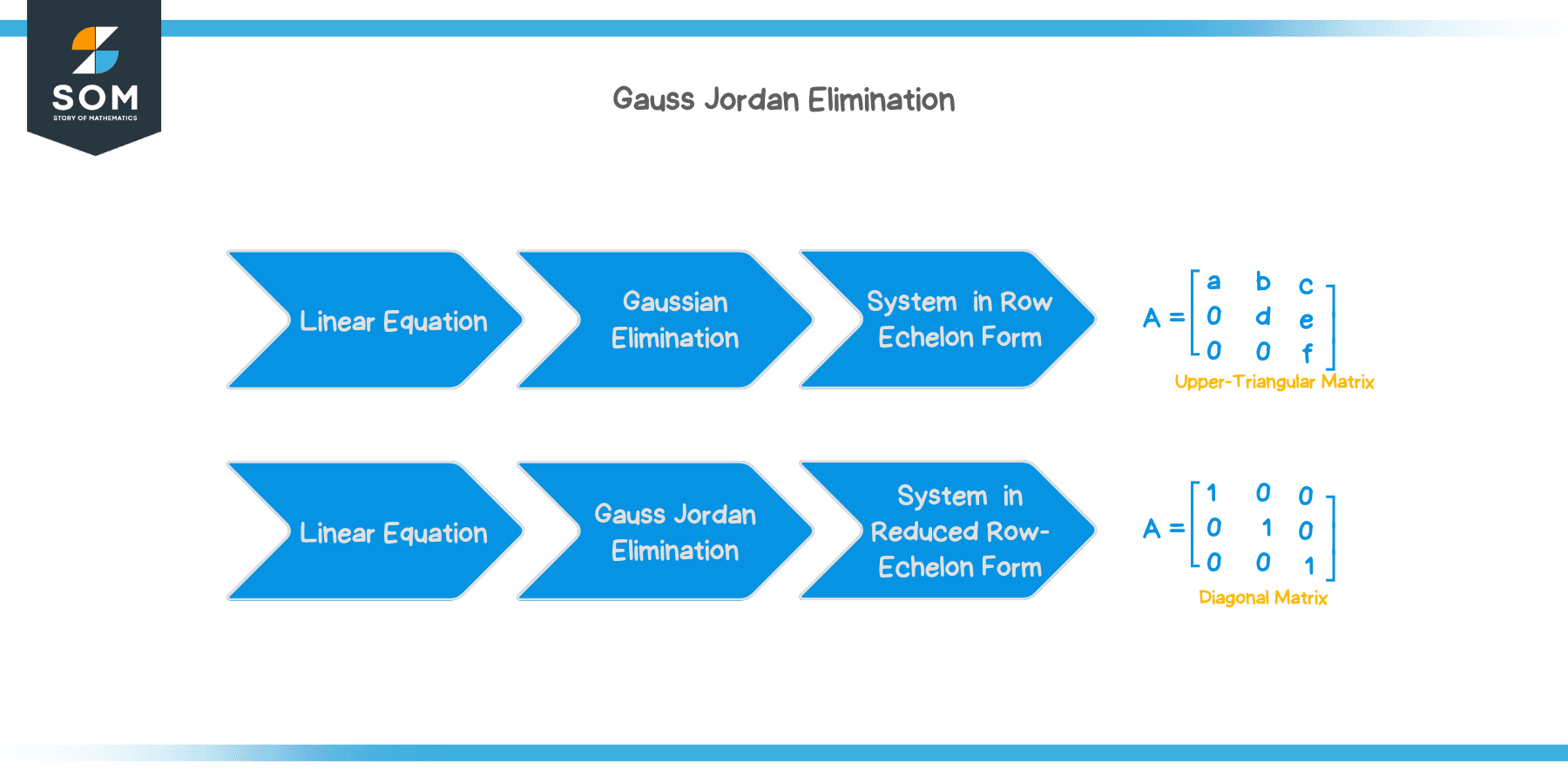
The Gauss Jordan Elimination, or Gaussian Elimination, is an algorithm to solve a system of linear equations by representing it as an augmented matrix, reducing it using row operations, and expressing the system in reduced row-echelon form to find the values of the variables.
In this lesson, we will see the details of Gaussian Elimination and how to solve a system of linear equations using the Gauss-Jordan Elimination method. Examples and practice questions will follow.
Gaussian Elimination is a structured method of solving a system of linear equations. Thus, it is an algorithm and can easily be programmed to solve a system of linear equations. The main goal of Gauss-Jordan Elimination is:
Let’s see what an augmented matrix form is, the $ 3 $ row operations we can do on a matrix and the reduced row echelon form of a matrix.
A system of linear equations is shown below:
$ \begin 2x + 3y &= \,7 \\ x – y &= 4 \end $
We will write the augmented matrix of this system by using the coefficients of the equations and writing it in the style shown below:
$ \left[ \begin < r r | r >2 & 3 & 7 \\ 1 & -1 & 4 \end \right] $
An example using $ 3 $ simultaneous equations is shown below:
$ \begin 2x + y + z &= \,10 \\ x + 2y + 3z &= 1 \\ – x – y – z &= 2 \end $
Representing this system as an augmented matrix:
$ \left[ \begin < r r r | r >2 & 1 & 1 & 10 \\ 1 & 2 & 3 & 1 \\ – 1 & – 1 & – 1 & 2 \end \right] $
There are $ 3 $ elementary row operations that we can do on matrices. It won’t change the solution of the system. They are:
The Gauss Jordan Elimination’s main purpose is to use the $ 3 $ elementary row operations on an augmented matrix to reduce it into the reduced row echelon form (RREF). A matrix is said to be in reduced row echelon form , also known as row canonical form, if the following $ 4 $ conditions are satisfied:
There aren’t any definite steps to the Gauss Jordan Elimination Method, but the algorithm below outlines the steps we perform to arrive at the augmented matrix’s reduced row echelon form.
At first glance, it’s not that easy to memorize/remember the steps. It’s a matter of solving several problems until you get the hang of the process. There is also the factor of intuition that plays a B-I-G role in performing the Gauss Jordan Elimination.
Let’s take a few examples to elucidate the process of solving a system of linear equations via the Gauss Jordan Elimination Method .
Solve the system shown below using the Gauss Jordan Elimination method:
The first step is to write the augmented matrix of the system. We show this below:
$ \left[ \begin < r r | r >– 1 & 2 & – 6 \\ 3 & -4 & 14 \end \right] $
Now, our task is to reduce the matrix into the reduced row echelon form (RREF) by performing the $ 3 $ elementary row operations.
The augmented matrix that we have is:
$ \left[ \begin < r r | r >– 1 & 2 & – 6 \\ 3 & – 4 & 14 \end \right] $
Step 1:
We can multiply the first row by $ – 1 $ to make the leading entry $ 1 $. Shown below:
$ \left[ \begin < r r | r >1 & – 2 & 6 \\ 3 & – 4 & 14 \end \right] $
Step 2:
We can now multiply the first row by $ 3 $ and subtract it from the second row. Shown below:
$ = \left[ \begin < r r | r >1 & – 2 & 6 \\ 0 & 2 & – 4 \end \right] $
We have a $ 0 $ as the first entry of the second row.
Step 3:
To make the second entry of the second row $ 1 $, we can multiply the second row by $ \frac< 1 > < 2 >$. Shown below:
$ = \left[ \begin < r r | r >1 & – 2 & 6 \\ 0 & 1 & – 2 \end \right] $
Step 4:
We are almost there!
The second entry of the first row should be $ 0 $. In order to do that, we multiply the second row by $ 2 $ and add it to the first row. Shown below:
$ = \left[ \begin < r r | r >1 & 0 & 2 \\ 0 & 1 & – 2 \end \right] $
This is the reduced row echelon form. From the augmented matrix, we can write two equations (solutions):
$ \begin x + 0y &= \, 2 \\ 0x + y &= -2 \end $
Thus, the solution of the system of equations is $ x = 2 $ and $ y = – 2 $.
Solve the system shown below using the Gauss Jordan Elimination method:
$ \begin x + 2y &= \, 4 \\ x – 2y &= 6 \end $
Let’s write the augmented matrix of the system of equations:
$ \left[ \begin < r r | r >1 & 2 & 4 \\ 1 & – 2 & 6 \end \right] $
Now, we do the elementary row operations on this matrix until we arrive in the reduced row echelon form.
We multiply the first row by $ 1 $ and then subtract it from the second row. This is basically subtracting the first row from the second row:
$ \left[ \begin < r r | r >1 & 2 & 4 \\ 1 – 1 & – 2 – 2 & 6 – 4 \end \right] $
$ =\left[ \begin < r r | r >1 & 2 & 4 \\ 0 & – 4 & 2 \end \right] $
We multiply the second row by $ -\frac< 1 >< 4 >$ to make the second entry of the row, $ 1 $:
$\left[ \begin < r r | r >1 & 2 & 4 \\ 0 \times -\frac< 1 > < 4 >& – 4 \times -\frac< 1 > < 4 >& 2 \times -\frac< 1 > < 4 >\end \right] $
$ =\left[ \begin < r r | r >1 & 2 & 4 \\ 0 & 1 & -\frac< 1 > < 2 >\end \right] $
Lastly, we multiply the second row by $ – 2 $ and add it to the first row to get the reduced row echelon form of this matrix:
$\left[ \begin < r r | r >1+(- 2\times 0) & 2+( – 2 \times 1) & 4 + ( – 2 \times -\frac< 1 > < 2 >) \\ 0 & 1 & -\frac< 1 > < 2 >\end \right] $
$=\left[ \begin < r r | r >1 & 0 & 5 \\ 0 & 1 & -\frac< 1 > < 2 >\end \right] $
This is the reduced row echelon form. From the augmented matrix, we can write two equations (solutions):
Thus, the solution of the system of equations is $ x = 5 $ and $ y = -\frac< 1 > < 2 >$.